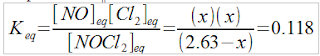Summer 2012 grades posted

Hmm, not sure I need to say more than what's in the title of the post. I submitted grades to the eServices system, they'll be visible to you whenever all the correct electrons flow through all the correct wires to make the interwebs update to display your grades.

I hope everyone had a useful class this summer, let me know if you have any questions and enjoy the rest of your summer.

Corrections to Exam 4 key

Typing up the key late at night was not a good idea... There were a number of errors on page 4 of the Exam 4 key that I posted this morning. If you already looked at the key or printed it out, throw away page 4 and go get a fresh version. Sorry about that. http://www.drbodwin.com/teaching/exams/c210pe4ak.pdf

Exams posted

All the exams we've taken for the summer 2012 class and their keys are posted on my web page, both on the "General Chemistry" page (http://www.drbodwin.com/teaching/genchem.php) and in the "Exam Archive" (http://www.drbodwin.com/teaching/examarchive.php). Let me know if you have questions.

Redox reactions

We looked at a few redox reactions today in class, some of you wanted the solutions posted. Enjoy.

For each pair of half cells, write the balanced spontaneous (standard) reaction and calculate the spontaneous (standard) cell voltage. {Actually, you'd do the secondpart of that process before you could do the first part}

Cu⁺¹|Cu (E⁰_red= +0.521V) and Fe³⁺|Fe²⁺(E⁰_red= +0.771V)

Cu half must be reversed to be the oxidation half rxn

E⁰_cell = E⁰_red+ E⁰_ox = 0.771V + (-0.521V) = +0.250V

Cu(s) ⇄ Cu⁺¹(aq) + 1e^⊖(aq)

1e^⊖ + Fe³⁺(aq) ⇄ Fe²⁺(aq)

------------------------------------------------------------------

Cu(s) + Fe³⁺(aq) ⇄ Fe²⁺(aq) + Cu⁺¹(aq)

BrO₃^-1|Br₂(E⁰_red= +1.478V) and Pt²⁺|Pt (E⁰_red= +1.188V)

Pt half must be reverse to be the oxidation half rxn

E⁰_cell = E⁰_red+ E⁰_ox = 1.478V + (-1.188V) = +0.290V

5 { Pt(s) ⇄ Pt⁺²(aq) + 2e^⊖(aq) }

12 H^⊕(aq) + 10e^⊖(aq) + 2 BrO₃^-1(aq) ⇄ Br₂(l) + 6 H₂O(l)

------------------------------------------------------------------

12 H^⊕(aq) + 5 Pt(s) + 2 BrO₃^-1(aq) ⇄ Br₂(l) + 5 Pt⁺²(aq) + 6 H₂O(l)

Cr⁺²|Cr (E⁰_red= -0.403V) and Pb⁺⁴|Pb⁺²(E⁰_red= +1.69V)

Cr half must be reverse to be the oxidation half rxn

E⁰_cell = E⁰_red+ E⁰_ox = 1.69V + (0.403V) = +2.09V

Cr(s) ⇄ Cr⁺²(aq) + 2e^⊖(aq)

2e^⊖ + Pb⁺⁴(aq) ⇄ Pb⁺²(aq)

------------------------------------------------------------------

Cr(s) + Pb⁺⁴(aq) ⇄ Pb²⁺(aq) + Cr⁺²(aq)

TeO₂|Te (E⁰_red= +0.604V) and Se|H₂Se (E⁰_red= -0.115V)

Se half must be reverse to be the oxidation half rxn

E⁰_cell = E⁰_red+ E⁰_ox = 0.604V + (0.115V) = +0.719V

2 { H₂Se(aq) ⇄ Se(s) + 2e^⊖(aq) + 2 H^⊕(aq) }

4 H^⊕(aq) + 4e^⊖ + TeO₂(s) ⇄ Te(s) + 2 H₂O(l)

------------------------------------------------------------------

4 H^⊕(aq) + 2 H₂Se(aq) + TeO₂(s) ⇄ Te(s) + 2 Se(s) + 4 H^⊕(aq) + 2 H₂O(l)

2 H₂Se(aq) + TeO₂(s) ⇄ Te(s) + 2 Se(s) + 2 H₂O(l)

MnO₄^-1|Mn⁺²(E⁰_red= +1.23V) and ClO₄^-1|ClO₃^-1(E⁰_red= +1.201V)

Cl half must be reverse to be the oxidation half rxn

E⁰_cell = E⁰_red+ E⁰_ox = 1.23V + (-1.201V) = +0.03V

5 { H₂O(l) + ClO₃^-1(aq) ⇄ ClO₄^-1(aq) + 2e^⊖(aq) + 2 H^⊕(aq) }

2 { 8 H^⊕(aq) + 5e^⊖ + MnO₄^-1(aq) ⇄ Mn²⁺(aq) + 4 H₂O(l) }

------------------------------------------------------------------

616H^⊕(aq) + 5 H₂O(l) + 2 MnO₄^-1(aq) + 5 ClO₃^-1(aq) ⇄ 5 ClO₄^-1(aq) + 2 Mn²⁺(aq) + 38H₂O(l) + 10 H^⊕(aq)

6 H^⊕(aq) + 5 H₂O(l) + 2 MnO₄^-1(aq) + 5 ClO₃^-1(aq) ⇄ 5 ClO₄^-1(aq) + 2 Mn²⁺(aq) + 3 H₂O(l)

Titrations are AWESOME!!

We looked at titrations today. Remember, titrations are just stoichiometry problems applied to a specific system/type of problem, they're not completely new information, approach them the same way you would approach any other stoichiometry problem:

1. Write a balanced chemical equation

2. Convert whatever you know the most about to moles

3. Using the mole ratio from the balanced chemical equation, convert moles of what you know to moles of what you're looking for

4. Convert moles of what you're looking for into whatever you want to know about it (grams, volume, concentration, etc.)

5. Check that your answer is reasonable (if possible)

On to today's problems...

30.00mL of 0.713M HNO₂(aq) is titrated to the equivalence point with 28.43mL of NaOH(aq) of an unknown concentration. What is the concentration of the NaOH(aq) stock solution? What was the pH of the HNO₂(aq) solution before the titration begins? What is the pH at the equivalence point? {K_a(HNO₂) = 4.0x10^-4}

HNO₂(aq) + NaOH(aq) ⇄ H₂O(l) + NaNO₂(aq)

(0.03000L HNO₂(aq)) (0.713M HNO₂(aq)) = 0.02139mols HNO₂

(0.02139mols HNO₂) (1mol NaOH / 1mol HNO₂) = 0.02139mols NaOH

(0.02139mols NaOH) / (0.02843L NaOH(aq)) = 0.752M NaOH(aq)

NaOH(aq) should be slightly more concentrated than HNO₂(aq), so this answer is reasonable

Before the titration begins, this is an aqueous solution of a weak acid, so we can calculate the pH using a K_a-type approach. Setting up a table...

	HNO2(aq) +	H2O(l) ⇄	H3O+(aq) +	NO2-1(aq)
[ ]initial	0.713M	XXXX	0	0
Δ[ ]	- x	XXXX	+ x	+ x
[ ]equilibrium	(0.713 – x) M	XXXX	x M	x M

Assuming that “x” is much less than 0.713, the K_a expression simplifies to:

K_a = (x)(x) / (0.713) = 4.0x10^-4

x = 0.01689 = [H₃O⁺]

pH = -log[H₃O⁺] = -log(0.01689) = 1.77

At the equivalence point, all of the HNO₂(aq) that was originally in the reaction has reacted with OH^-1(aq) to form nitrite ions, NO₂^-1(aq). The titration started with:

(0.03000L HNO₂(aq)) (0.713M HNO₂(aq)) = 0.02139mols HNO₂

So at the equivalence point we have a solution that contains 0.02139mols of NO₂^-1(aq) in (30.00mL + 28.43mL = 58.43mL) of solution. The concentration of NO₂^-1(aq) at the equivalence point is:

(0.02139mols of NO₂^-1(aq)) / (0.05843L) = 0.3659M NO₂^-1(aq)

This can now be plugged in to a K_b-type equilibrium to solve...

	NO2-1(aq) +	H2O(l) ⇄	OH-1(aq) +	HNO2(aq)
[ ]initial	0.3659M	XXXX	0	0
Δ[ ]	- x	XXXX	+ x	+ x
[ ]equilibrium	(0.3659 – x) M	XXXX	x M	x M

Assuming that “x” is much less than 0.3659, the K_b expression simplifies to:

K_b = (x)(x) / (0.3659) = 2.5x10^-11

x = 3.02x10^-6 = [OH^-1]

pOH = -log[OH^-1] = -log(3.02x10^-6) = 5.519

pH = 14 – 5.519 = 8.48

15.00mL of sulfurous acid of unknown concentration is titrated to the second equivalence point with 23.18mL of 0.332M NaOH(aq). What is the concentration of the sulfurous acid stock solution?

H₂SO₃(aq) + 2 NaOH(aq) ⇄ H₂O(l) + Na₂SO₃(aq)

(0.02318L NaOH(aq)) (0.332M NaOH(aq)) = 7.696x10^-3mols NaOH

(7.696x10^-3mols NaOH) (1mol H₂SO₃/ 2mol NaOH) = 3.848x10^-3mols H₂SO₃

(3.848x10^-3mols H₂SO₃) / (0.01500L H₂SO₃(aq)) = 0.257M H₂SO₃(aq)

NaOH(aq) should be slightly more concentrated than H₂SO₃(aq), so this answer is reasonable

I'll be in tomorrow morning, let me know if you have any questions.

Crunching through K_a problems...

4. What is the expected pH of a 2.49M solution of acetic acid {K_a= 1.8x10^-5}? What is the expected pH when 100.0mL of this solution is combined with 100.0mL of water? Assume volumes are additive.

This is a K_a-type equilibrium problem, organize the information using a table.

	HC2H3O2(aq) +	H2O(l) ⇄	H3O+(aq) +	C2H3O2-1(aq)
[ ]initial	2.49 M	XXXX	0 M	0 M
Δ[ ]	- x	XXXX	+ x	+ x
[ ]equilibrium	(2.49 – x) M	XXXX	x M	x M

Assume “x” is much smaller than 2.49, plug in to the equilibrium constant expression...

x = 6.69x10^-3 = [H₃O⁺¹]

Assumption is good.

pH = -log[H₃O⁺¹] = -log(6.69x10^-3) = 2.174

For the second part, the set-up is the same, the only difference is that the initial concentration of acetic acid has been diluted. Calculating the dilution...

C₁V₁= C₂V₂

(2.49M)(100.0mL) = C₂(200.0mL)

C₂= 1.245M

Plug in and solve the same way:

x = 4.73x10^-3 = [H₃O⁺¹]

Assumption is still good.

pH = -log[H₃O⁺¹] = -log(4.73x10^-3) = 2.325

5. A 1.83M solution of a weak, monoprotic acid {HA(aq)} has a pH of 3.48. What is the K_a of this acid?

We can approach this as a K_a-type equilibrium problem as well, organize the information using a table.

	HA(aq) +	H2O(l) ⇄	H3O+(aq) +	A-1(aq)
[ ]initial	1.83 M	XXXX	0 M	0 M
Δ[ ]	- x	XXXX	+ x	+ x
[ ]equilibrium	(1.83 – x) M	XXXX	x M	x M

In this case, we are given a pH, which gives us a way to calculate [H₃O⁺], which gives us “x”...

[H₃O⁺] = 10^-pH = 10^-3.48 = 3.3113x10^-4 (Assumption is good.)

K_a= (3.3113x10^-4)(3.3113x10^-4) / (1.83) = 5.99x10^-8

6. You have combined 100.0mL of 2.84M hydrofluoric acid {K_a = 6.8x10^-4} and 100.0mL of 2.19M fluoride ions. What is the expected pH of the resulting solution? Assume volumes are additive.

Again, we can approach this as a K_a-type equilibrium problem (Noticing a pattern here?), organize the information using a table.

	HF(aq) +	H2O(l) ⇄	H3O+(aq) +	F-1(aq)
[ ]initial	1.42 M	XXXX	0 M	1.095 M
Δ[ ]	- x	XXXX	+ x	+ x
[ ]equilibrium	(1.42 – x) M	XXXX	x M	(1.095 + x) M

A couple little adjustments in this case... the original concentrations given in the problem have to be diluted to get the “initial” concentrations in the table. The other key difference here is that we're starting out with a mixture of reactants and products. That might clutter up the math a little bit, but it doesn't really change the way we approach the problem. To simplify things, let's assume that “x” is small compared to both 1.42 and 1.095. Then the K_a expression is:

6.8x10^-4= (x)(1.095) / (1.42)

x = 8.818x10^-4

Assumption is good.

pH = -log[H₃O⁺¹] = -log(8.818x10^-4) = 3.055

Problem 3 (2012-07-09)

14.78g PCl₅(g) and 10.15g O₂(g) are combined in a 1.500L vessel and reach equilibrium with POCl₃(g) and ClO(g). If K = 8.53x10^-9, find all equilibrium concentrations.

	2 PCl5(g) +	3 O2(g) ⇄	2 POCl3(g) +	4 ClO(g)
[ ]initial	(14.78g / 208.239g/mol) / 1.500L = 0.047317M	(10.15g / 31.998g/mol) / 1.500L = 0.21147M	0 M	0 M
Δ [ ]	– 2x M	– 3x	+ 2x	+ 4x M
[ ]equilibrium	(0.047317 – 2x) M	(0.21147 – 3x) M	2x M	4x M

Plugging in to the equilibrium constant expression...

Solving this directly would be rough, so let's try a simplifying approximation. Since the equilibrium is quite reactant-favored, we can assume that 2x is small compared to 0.047317 and 3x is small compared to 0.21147. We need to check this later, but that will simplify the equilibrium constant expression to:

x⁶ = 1.76376x10^-16

x = 0.002368

BEFORE WE GO ANY FARTHER, CHECK THE ASSUMPTION WE MADE!! 2x = 0.0047, this is (0.0047/0.047317)*100 = 9.9%. This is a little too high for this assumption to work well. Oops. Don't worry, I don't expect anyone to solve a 6^th order polynomial on an exam, these numbers are a little off because I made this problem up during class. For numbers that work, try using K = 8.53x10^-12. , then x = 7.489x10^-4 and the assumption is OK. If you'd like to know how to solve the original problem, you could use the method of successive approximations, this was how I had to treat these problems when I was an undergrad taking Gen Chem.

Exam tomorrow, if you have questions let me know, I should be online until at least 7 or 8pm tonight.

Exam 1 and Key posted

Exam 1a and the key are posted at http://www.drbodwin.com/teaching/genchem.php, also linked in the exam archive.  


Enjoy the lovely weekend.

Second in-class problem from 2012-07-05

1.92M NF₃(g) + 1.63M O₂(g) → NOF₃(g) K_eq=1.74x10⁹, find all [ ]_eq

	2 NF3(g) +	O2(g) ⇄	2 NOF3(g)
[ ]initial	1.92 M	1.63 M	0 M
Δ [ ]	- 2x M	- x M	+ 2x M
[ ]equilibrium	(1.92 – 2x) M	(1.63 – 2x) M	2x M

Plugging in to the equilibrium constant expression, this would get ugly pretty quickly. Let's try to simplify it with an approximation. Since K_eqis quite product-favored, we can probably assume that the limiting reagent is essentially used up to form (almost) the theoretical yield of product. From the balanced chemical equation, we need 2 NF₃(g) for each O₂(g), but we didn't start with twice as much NF₃(g), so that must be the limiting reactant. For every mole of NF₃(g) that reacts, 1 mol of NOF₃(g) is formed, so the equilibrium concentration of NOF₃(g) will be (just a tiny bit less than) 1.92M. To make (just a tiny bit less than) 1.92M NOF₃(g), we need halfthat amount of O₂(g), so to reach equilibrium we will consume (very close to) 0.96M O₂(g), leaving (1.63M – 0.96M = 0.67M) of O₂(g) at equilibrium.

{NOTE: If you prefer, you could explicitly calculate this out using our standard 4-step process for limiting reactants/theoretical yields by assuming a volume. I'd assume 1L to make the calculations easier.}

We can now start with a fresh table to organize our information...

	2 NF3(g) +	O2(g) ⇄	2 NOF3(g)
[ ]equilibrium	“a tiny bit”	0.67 M	1.92 M

Now we can plug into the equilibrium constant expression:

Solving, “a tiny bit” = 5.62x10^-5M. Make sure you always CHECK YOUR ASSUMPTIONS! In this case, yes, 5.62x10^-5 is indeed very small compared to 1.92, so the assumption is valid. One of the nice things about equilibrium problems is that you can always plug your results back in to the equilibrium constant expression and see if you get an answer that's close to what's given in the problem. In this case...

(1.92)² / {5.62x10^-5)²(0.67) = 1.742x10⁹

So...

[NF₃]_eq= 5.62x10^-5 M

[O₂]_eq= 0.67M

[NOF₃]_eq= 1.92M

First in-class problem from 2012-07-05

2.63M NOCl₂(g) → NO(g) + Cl₂(g) K=0.118, find all [ ]_eq

	NOCl2(g) ⇄	NO(g) +	Cl2(g)
[ ]initial	2.63 M	0 M	0 M
Δ [ ]	- x M	+ x M	+ x M
[ ]equilibrium	(2.63 – x) M	x M	x M

Plugging in to the equilibrium constant expression...

Because the value of K is not exceptionally large or exceptionally small, this one will probably require working through the quadratic. Breaking it down in steps...

(x)(x) = 0.118(2.63-x)

x² = 0.31034 – 0.118x

x² + 0.118x + (-0.31034) = 0

Plugging in to the quadratic formula:

NOTE: The other root is negative, it doesn't work in this problem.

[NOCl₂]_eq= 2.63 – 0.50 = 2.13M

[NO]_eq = x = 0.501M

[Cl₂]_eq= x = 0.501M

Problem Set Answers (2012-07-02)

Chem 210 - Summer 2012 - Problem Set {2012-07-02}

1. A 395.4g block of glass (heat capacity = 0.84J/g.K) warms from -42.37℃ to 20.53℃. How much energy/heat has been transferred? Is this process endothermic or exothermic? If the energy/heat gained or lost by the glass block is transferred from/to a 528.7g block of copper (heat capacity = 0.385J/g.K) initially at 15.39℃, what is the final temperature of the copper block?

(0.84J/g•K)(395.4g)(62.90K)  =  20891J  →  20.9kJ

If the glass block is warming, then energy/heat is being absorbed by the block, this is an endothermic process.

(0.385J/g•K)(528.7g)(ΔT)  =  20891J

ΔT  =  102.6°C

Since the glass block is absorbing heat (endothermic), the copper block must be releasing heat and getting colder.

15.39°C – 102.6°C  =  -87.2°C

2. You have dissolved 12.482g of aluminum nitrate in enough water to make 150.0mL of solution. What is the molarity of aluminum ions in the resulting solution? What is the molarity of nitrate ions in the resulting solution?
First, find the molarity of the whole aluminum nitrate

(12.482g) / (212.994g/mol)  =  0.0586026mols Al(NO₃)₃

(0.0586026mols Al(NO₃)₃) / (0.1500L)  =  0.390684M Al(NO₃)₃ (aq)

For every mol of Al(NO₃)₃ that dissolves, there is 1 mol of Al⁺³(aq). Converting…

(0.390684mols Al(NO₃)₃ / L) (1mol Al⁺³(aq) / mols Al(NO₃)₃)  =  0.3907M Al⁺³(aq)

For every mol of Al(NO₃)₃ that dissolves, there are 3 mol of NO₃^-1(aq). Converting…

(0.390684mols Al(NO₃)₃ / L) (3mol NO₃^-1(aq) / mols Al(NO₃)₃)  =  1.1721M NO₃^-1(aq)

3. What is the freezing point of a solution made from 7.113g of potassium sulfate dissolved in 75.00mL of water?
Calculate the molality of potassium sulfate:

(7.113g) / (174.258g/mol)  =  0.040819mols K₂SO₄

(0.040819mols K₂SO₄) / (0.07500kg)  =  0.54425m K₂SO₄(aq)

Plugging in to the freezing point depression equation:

ΔT_fp = k_fpd • m • i

ΔT_fp  =  (1.86°C/m)(0.54425m)(3)  =  3.04°C

The freezing point of the solution is depressed by 3.04°C. Since the freezing point of pure water is 0°C, the freezing point of the solution should be -3.04°C.  

4. Ammonia gas reacts with chlorine gas to form nitrogen trichloride gas and hydrogen gas. At some point, 53.65mg of nitrogen trichloride is formed in 28.63 seconds in a 12.00L reaction vessel. What is the rate of the reaction? What are the rates of consumption and production for each reactant and product in the mixture?
The only thing we have any information about is NCl₃, so let’s start by calculating the rate of formation of NCl₃ …

Rate_NCl3  =  { (0.05365g NCl₃ / 120.366g/mol) / (12.00L) } / 28.63sec  =  1.297x10^-6 M/sec

Now we need the balanced chemical equation:

2 NH₃(g)  +  3 Cl₂(g)  →  2 NCl₃(g)  +  3 H₂(g)

Rate_rxn should be half the rate of production of NCl₃ , so (1.297x10^-6 M/sec) / 2  =  6.487x10^-7 M/sec

Rate_NH3 should be the same as the rate of production of NCl₃ or 2xRate_rxn, 1.297x10^-6 M/sec

Rate_Cl2 should be three times Rate_rxn, 3(6.487x10^-7 M/sec) = 1.946x10^-6 M/sec

Rate_H2 should be three times Rate_rxn, 3(6.487x10^-7 M/sec) = 1.946x10^-6 M/sec

5. You are studying the reaction of sulfur dioxide gas with hydrogen chloride gas to form thionyl chloride {SOCl₂(g)} and water gas at 6.48℃. You've completed the following reactions:

Rxn #	[sulfur dioxide]0	[hydrogen chloride]0	Initial Rate (M/min)
1	0.429	0.317	3.02x10-5
2	0.858	0.317	1.21x10-4
3	0.429	0.951	9.06x10-5

What is the rate law expression for this reaction? Include the rate law constant. If Rxn #3 is repeated at 28.81℃, the rate increases to 4.67x10^-3 M/min. What is the activation energy for this process?
Comparing Rxn #1 and #2, doubling [SO₂]₀ quadruples the initial rate  →  2nd order with respect to [SO₂]₀
Comparing Rxn #1 and #3, tripling [HCl]₀ triples the initial rate  →  1st order with respect to [HCl]₀
The rate law expression is:

Rate₀  =  k [SO₂]₀² [HCl]₀¹

Plugging in conditions for Rxn #1 (or any of them…) to get the value of “k”:

3.02x10^-5 M/min  =  k (0.429M)² (0.317M)

k  =  5.176x10^-4 M^-2min^-1

For the new temperature, we need a new value of “k”, plugging in we get…

4.67x10^-3 M/min  =  k (0.429M)² (0.951M)

k  =  2.668x10^-2 M^-2min^-1

Plugging in to the comparative form of the Arrhenius equation:

ln (k₁/k₂)  =  (E_a/R) {(1/T₂) – (1/T₁)}

ln (5.176x10^-4 M^-2min^-1 / 2.668x10^-2 M^-2min^-1)  =  (E_a / 8.314J/mol•K) {(1/301.96K) – (1/279.63K)}

E_a  =  123.9kJ/mol

Any questions? Let me know.

Preparing for exams (Summer 2012)

A few people have asked about the best way to prepare for exams this summer. Preparing for exams in summer is really no different than preparing for exams during the regular year, so this advice works for any time.
1. Review class notes and problems we did in class.
2. For topics you feel pretty confident about, take a look at one or two related problems from your textbook to make sure you're in good shape.
3. For topics that you're a little more shaky on, look over the relevant section of your textbook and follow along with the worked out problems in the text. Then try a couple of the end of chapter problems.
4. After you've reviewed the material from class and your textbook, take a look at a previous exam posted on my web page (http://www.drbodwin.com/teaching/examarchive.php) and see if you've got the concepts and problems figured out. Using the exam, identify your weak spots and go back to your textbook to brush up.
5. If you have questions, ask. Check the blog (that's where you are right now!) to see if there is already an answer posted.


The only thing that's slightly different about the summer class is the way the topics are distributed on exams. In a typical spring semester, Exam #1 covers states of matter, gas laws, solution, colligative properties, and maybe a couple other assorted topics. Exam #2 covers kinetics and equilibrium. For the summer class, Exam #1 hits states of matter, gas laws, solution, colligative properties, and kinetics. If you're looking at an Exam #2 from a spring semester and a question seems totally unfamiliar, it might be an equilibrium question, we'll get to that after this week's exam.


We haven't talked about mechanisms and catalysts in class yet, we'll get to those tomorrow (Monday), so they will be on the exam.


Enjoy the rest of your weekend and let me know if you have any other questions.