Pre-Exam 3 email questions...

A few questions have come in by email, here they are:

----Question-----

I have a question regarding problem 9 on exam 3a from spring 2013. I understand that the calculated x value doesn't fit under the assumptions. I see where the first two values come from. I was wondering where the -1.238 x 10^-3 came from?

{(x)(x)} / (0.516 – x) = 2.40 x 10^-3

0.516 is the initial concentration and 2.40 x 10^-3 is Ka.

 x^2 + (2.40 x 10^-3)x + (-1.238 x 10^-3 ) = 0

----Answer-----

In order to use the quadratic formula, we have to solve the equation to the form:

ax² + bx + c = 0

The (-1.238x10^-3) term comes from (2.40x10^-3)(0.516).

----Question-----
I was going through some of the old exams and the problems that use the Henderson - Hasselbalch. In those examples when it asked for the concentration of the conjugate base over the concentration of conjugate acid, but in the key only the moles of both are put in those places. Why? 
----Answer-----

This is a little mathematical shortcut. Since both the conjugate acid and conjugate base are in the same total volume of solution, the volumes mathematically cancel so I left them out. For example, if we had a buffer made from 0.65mols of HA and 0.55mols of A^-1 in 800.0mL of buffer solution, that last part of the Henderson-Hasselbalch would look like:

You can always keep the volume in there and calculate the actual concentrations of each component, you should get exactly the same answer either way.

----Question-----
I dont understand how you can derive pH values from pka's given in the question. I also dont understand how pH can be calculated at each eq point in the titration curve as in number 11 on spring 2013 where it asks what indicator to use.. it says use the 2 pkas...how does this help?
----Answer-----

There are a couple ways that pK_a (or pK_b) can lead to a pH. One possibility is in a question like "What is the expected pH of a 0.618M solution of ammonium nitrate solution?" In this question, you can set up a K_a-type equilibrium for ammonium ions and use the K_a of ammonium to calculate [H₃O⁺] and pH. This is similar to the problem I posted yesterday (http://chemistryingeneral.blogspot.com/2014/03/neutral-salts.html). This method can be used to calculate the initial pH for a titration. It would also work to approximate the pH of an equivalence point. Let's think about that...

For the titration of phosphite ions with hydrochloric acid, we can calculate the initial pH by setting up a K_b-type equililbrium and using the K_b of phosphite ion to calculate [OH^-1] and pOH and pH. At the first equivalence point in this titration, we have a solution that we can think of as HPO₃^-2(aq) because we have added just enough acid to complete the following equation exactly once:

PO₃^-3(aq) + H⁺(aq)  <=> HPO₃^-2(aq)

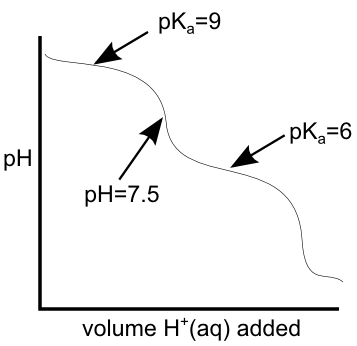
Between equivalence points, we have buffering regions of the titration curve... at the mid-point of this buffering region, the pH is equal to the pK_a of the weak acid of the mixture. If we know the pK_a (and therefore the pH) on either side of the equivalence point we're interested in, we can get a pretty reliable estimate of the pH of that equivalence point. On the titration curve below, if the pK_as that bound the equivalence point are 6 and 9, the pH of the equivalence point should be right between them at pH = 7.5.

Keep an eye on the weather... Unless MSUM officially closes campus tomorrow, we will have class and the exam as planned. I'll be there at 7:30.

Neutral salts

The conjugate of a strong acid or strong base is neutral. That's just something we tend to accept, memorize, and move on. But why? Those two words are a big part of the reason I'm a chemist.

Let's take a look at a strong acid and see if we can make sense of this. Of the typical strong acids, nitric is usually the weakest, and nitric is also the only one that might have a K_a listed in standard tables. The stronger strong acids have really useful K_a values listed in the tables like "large" or "strong"... I don't have a "large" button on my calculator, so let's just use nitric acid and we'll hopefully see why the other strong acids would follow the same trend if we had a value for their K_a.

The K_a for nitric acid is usually listed at around 25. That means the K_b for nitrate ions is:

That's a REALLY weak K_b, but we can go ahead and calculate the pH of a solution just like in any other situation. How about the problem: What is the expected pH of a 0.500M solution of sodium nitrate? {By the way, we could make similar arguments to show that the sodium ions don't affect the pH, but we'll save those for another day...} As with all good equilibrium problems, it's probably not a bad idea to start with a table:

Now we can set up the K_b expression and plug in the numbers we have:

We should be able to simplify that with some assumptions... Let's assume that "x" is much smaller than 0.500 and much larger than 10^-7. That gets us the simplified expression:

Solving this expression, we get x = 1.41x10^-8, which gives us a pOH = -log(1.41x10^-8) = 7.85, and pH = 6.15. Hmm, that's not neutral, that's acidic. The whole point of this was to prove that nitrate was a neutral ion. This is a disaster.

BUT WAIT!

We made some assumptions. We didn't check our assumption after we solved for "x". This is why I always tell you to check assumptions... We assumed that "x" would be much smaller than 0.500, which it is, but we also assumed that "x" was much larger than 10^-7, which it absolutely is not! So the assumptions we made were an oversimplification of the problem and that's where we entered the danger zone. Looking back at our K_b expression, we can only simplify it to:

That's still going to require the quadratic formula to solve. I'll let you work out the details, but the result should be that x = 7.96x10^-9. That means:

[OH^-1]eq = 10^-7 + (7.96x10^-9) = 1.08x10^-7 M

pOH = -log(1.08x10^-7) = 6.9667

pH = 14 - 6.9667 = 7.0333

That's not exactly 7.0000000000 neutral, but it's pretty darn close, especially if we're thinking about this in terms of selecting a visual acid-base indicator for a titration.